Series Temporales, Op. 2: DBSCAN
DBSCAN es un algoritmo no supervisado bastante popular. ¿Quieres aprender su funcionamiento y cómo afinarlo para un mejor desempeño en la detección de anomalías para series temporales?
Series Temporales, Op. 2: DBSCAN
En [1] se expuso el método estadístico ARIMA (siglas para AutoRegressive Integrated Moving Average) para la detección de anomalías en series temporales. En este artículo se va a hablar de los sistemas ML (siglas para Machine Learning), particularmente de DBSCAN (siglas para Density-Based Spatial Clustering of Applications with Noise). A diferencia de los primeros, asume que no es necesario conocer si los datos fueron generados por un modelo matemático específico, siempre y cuando puedan producirse predicciones acertadas [2][3]. Finalmente, se mostrará una tabla con diferentes ideas de aplicación (para series temporales) de este algoritmo y sus variantes.
DBSCAN
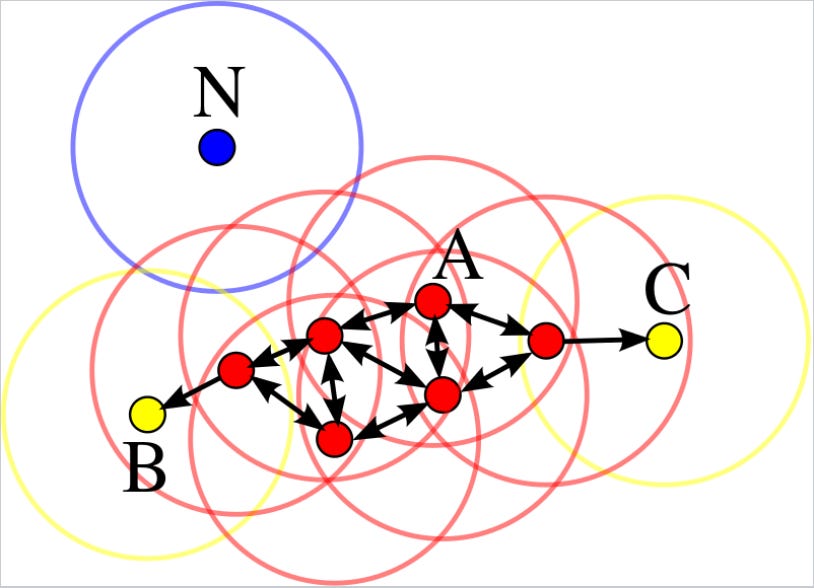
Es un algoritmo de agrupamiento basado en densidad [4][5]. Clasifica los datos en 3 categorías (ver Figura 1):
Núcleo: tienen el número mínimo de puntos (MinPts) que cumplen con una distancia (eps). Cada agrupamiento contiene al menos uno.
Borde: son datos “vecinos” de los de Núcleo. Actúan como una barrera porque no se pueden alcanzar más puntos a partir de ellos.
Anomalía: no pertenecen a ninguna de las otras clasificaciones.
Sus ventajas son [5]:
Identifica mejor las anomalías porque tiene la noción del ruido.
Puede formar agrupamientos de formas arbitrarias.
Al ser un algoritmo no supervisado, no es necesario conocer las clases de los agrupamientos por adelantado.
Sus desventajas son [6]:
No es determinista con los datos Borde. Cuando estos son alcanzables desde más de un agrupamiento, pueden clasificarse en cualquiera de ellos.
No agrupa bien los datos cuando hay mucha diferencia en las densidades.
Para afinar su funcionamiento, se tienen que especificar dos parámetros:
minPts: Es el número mínimo de datos que una agrupación debe tener para que se la considere densa. Si el conjunto de datos tiene más de 2 dimensiones (D) o también llamados atributos, se recomienda que minPts = 2*D [6][7].
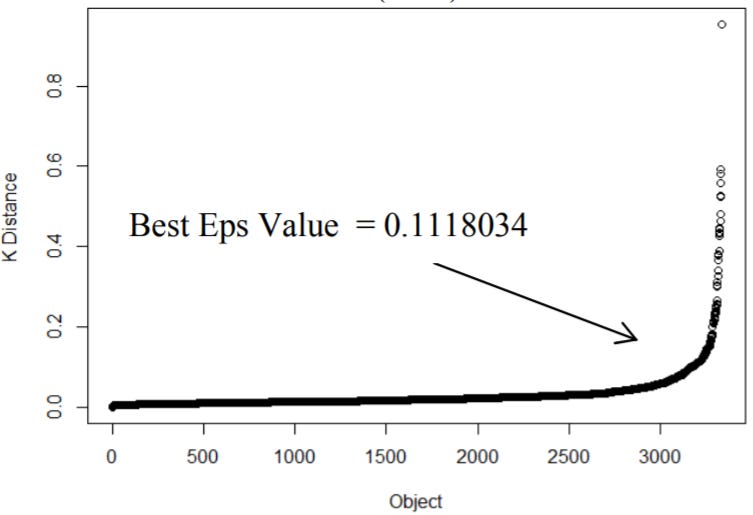
eps: Es la distancia máxima entre 2 datos para considerarlos dentro del mismo agrupamiento. Está directamente influenciado por la función de distancia que se elija (ej. Distancia euclidiana). Existe una técnica [8][9] que consiste en calcular la distancia promedio entre cada dato y sus k vecinos, en donde k = minPts. Luego, se visualiza el promedio en orden ascendente de estas distancias k. Siendo el valor óptimo eps donde se observe la máxima curvatura (ver Figura 2).
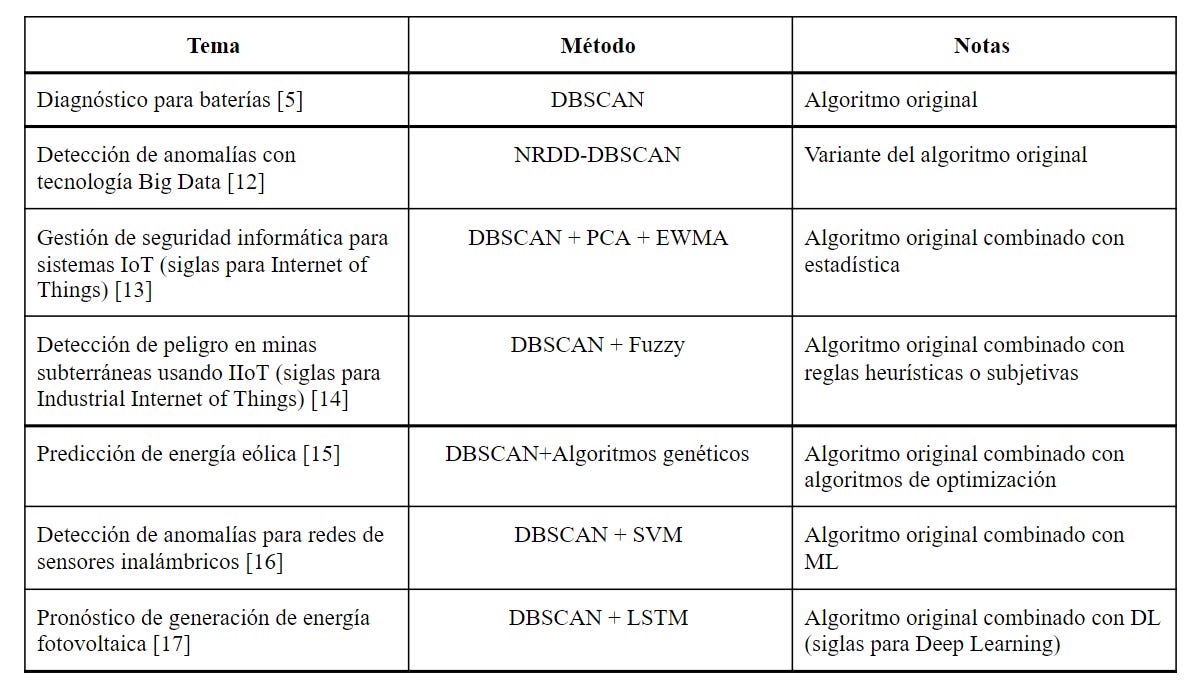
Ideas de aplicación para Perú
Algunas sugerencias de uso para DBSCAN (ver Tabla 1) son el proyecto Punta Lomitas [10] que consiste en un parque eólico ubicado en Ica. Adicionalmente, Perú es un país minero y cuenta con minas subterráneas ubicadas en diferentes departamentos [11].
Conclusiones
DBSCAN es un algoritmo ML de agrupamiento por densidad, que es robusto al ruido. Por ello es popular en la detección de anomalías. Para optimizar su desempeño se recomienda afinar los parámetros minPts y eps. Finalmente, cabe resaltar que no solamente puede emplearse en series temporales, sino también en aplicaciones de visión por ordenador por ejemplo.
Referencias
[1] R. Ayala Meza, “Series Temporales, Op. 1:ARIMA,” Data Science Research Peru, 2021. https://datasciencepe.substack.com (accessed Nov. 14, 2021).
[2] L. Breiman, “Statistical Modeling: The Two Cultures (with comments and a rejoinder by the author),” Stat. Sci., vol. 16, no. 3, pp. 199–231, Aug. 2001, doi: 10.1214/ss/1009213726.
[3] G. Papacharalampous, H. Tyralis, and D. Koutsoyiannis, “Comparison of stochastic and machine learning methods for multi-step ahead forecasting of hydrological processes,” Stoch. Environ. Res. Risk Assess., vol. 33, no. 2, pp. 481–514, 2019, doi: 10.1007/s00477-018-1638-6.
[4] Z. He, X. Xu, and S. Deng, “Discovering cluster-based local outliers,” Pattern Recognit. Lett., vol. 24, no. 9, pp. 1641–1650, 2003, doi: https://doi.org/10.1016/S0167-8655(03)00003-5.
[5] D. Li, Z. Zhang, P. Liu, and Z. Wang, “DBSCAN-Based Thermal Runaway Diagnosis of Battery Systems for Electric Vehicles,” Energies , vol. 12, no. 15. 2019, doi: 10.3390/en12152977.
[6] “DBSCAN,” Project Wikimedia, 2021. https://es.wikipedia.org/wiki/DBSCAN.
[7] J. Sander, X. Qin, Z. Lu, N. Niu, and A. Kovarsky, “Automatic Extraction of Clusters from Hierarchical Clustering Representations,” in Proceedings of the 7th Pacific-Asia conference on Advances in knowledge discovery and data mining, 2003, pp. 75–87, Accessed: Nov. 14, 2021. [Online]. Available: https://www.cs.toronto.edu/~nn/papers/PAKDD03.pdf.
[8] A. M. Sefidian, “How to determine epsilon and MinPts parameters of DBSCAN clustering.” https://sefidian.com/2020/12/18/how-to-determine-epsilon-and-minpts-parameters-of-dbscan-clustering/.
[9] N. Rahmah and I. Sukaesih, “Determination of Optimal Epsilon (eps) value on DBSCAN algorithm to clustering data on Peatland Hotspots in Sumatra,” IOP Conf. Ser. Earth Environ. Sci., vol. 31, 2016, doi: 10.1088/1755-1315/31/1/012012.
[10] “Engie inicia las obras del mayor parque eólico de Perú,” Windpower Monthly, 2021. https://www.worldenergytrade.com/energias-alternativas/energia-eolica/engie-inicia-las-obras-del-mayor-parque-eolico-de-peru.
[11] “Mapa de minería subterránea del Perú,” Mining suppliers Perú. http://miningsuppliersperu.com/mapa-de-mineria-subterranea-del-peru/.
[12] H. Ghallab, H. Fahmy, and M. Nasr, “Detection outliers on internet of things using big data technology,” Egypt. Informatics J., vol. 21, no. 3, pp. 131–138, 2020, doi: https://doi.org/10.1016/j.eij.2019.12.001.
[13] T. Qin, B. Wang, R. Chen, Z. Qin, and L. Wang, “IMLADS: Intelligent Maintenance and Lightweight Anomaly Detection System for Internet of Things,” Sensors , vol. 19, no. 4. 2019, doi: 10.3390/s19040958.
[14] Y. Peng, A. Tan, J. Wu, and Y. Bi, “Hierarchical Edge Computing: A Novel Multi-Source Multi-Dimensional Data Anomaly Detection Scheme for Industrial Internet of Things,” IEEE Access, vol. 7, pp. 111257–111270, 2019, doi: 10.1109/ACCESS.2019.2930627.
[15] P. Zhang, Y. Wang, L. Liang, X. Li, and Q. Duan, “Short-Term Wind Power Prediction Using GA-BP Neural Network Based on DBSCAN Algorithm Outlier Identification,” Processes , vol. 8, no. 2. 2020, doi: 10.3390/pr8020157.
[16] H. Saeedi Emadi and S. M. Mazinani, “A Novel Anomaly Detection Algorithm Using DBSCAN and SVM in Wireless Sensor Networks,” Wirel. Pers. Commun., vol. 98, no. 2, pp. 2025–2035, 2018, doi: 10.1007/s11277-017-4961-1.
[17] J. Zhang and Y. Zhang, “Forecast of photovoltaic power generation based on DBSCAN,” E3S Web Conf., vol. 236, 2021, [Online]. Available: https://doi.org/10.1051/e3sconf/202123602016.