Modelos ARIMA, SARIMA y Método de Selección de Variables LASSO para Series Temporales (Parte 2)

Los modelos ARIMA y SARIMA , son métodos utilizados para el análisis de una serie de tiempo y predicción de un estudio, aparte de ello existen otros métodos, así como el método de LASSO.

Autores: Gladys Choque Ulloa, Sandra Rosa Arroyo Paredes, Redy Rivas Idme

APLICACIÓN

Para la parte de aplicación se utilizó la base de datos del Instituto Nacional de Meteorología del Ministerio de Agricultura, Ganadería y Abastecimiento, del estado de Rio Grande del Sur, Brasil, en el período 2018-2021 [9], donde se uso 10 variables (Temperatura promedio, Precipitación, Presión, Tiempo de Rocío, Temperatura Máxima, Temperatura Mínima, Humedad, Humedad Mínima, Viento Máximo y Viento Promedio). Se hizo un ajuste de los modelos ARIMA, SARIMA y el método de selección de variables con LASSO, utilizando las pruebas de Dickey Fuller y Ljung Box, haciendo uso del lenguaje de programación R para estimar los coeficientes. Se realizó una comparación de estos modelos para determinar cuál es el más adecuado para representar la serie original y poder estimar valores futuros, observándose que el modelo SARIMA tiene un mejor ajuste y mejor predicción de su comportamiento. 

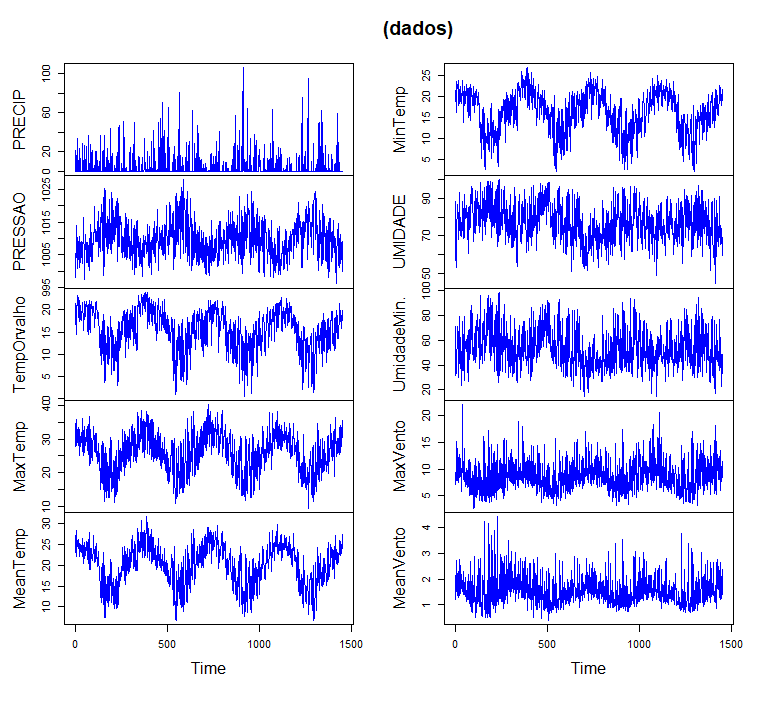
Figura 2: Gráfico de las series temporales para nuestras variables de estudio.Fuente: Elaboración propia.

En la figura 2, se puede observar el comportamiento de las series temporales de nuestras 10 variables de estudio con respecto al tiempo,  vemos que las series temporales presentan tendencia y no son estacionarias porque no tienen una media y varianza constante, por lo cual se aplicará diferencias a las series para que sean estacionarias y para comprobarlo se usará las pruebas de Dickey Fuller y  Ljung Box.

A partir del resultado de la prueba de Dickey Fuller, p-value : 0,01 < 0.05, podemos decir que hay suficiente evidencia para aceptar la hipótesis que la serie es estacionaria.

A partir de la función auto.arima considerando el penalizador de Critério de Información de Akaike (AIC) fue identificado que el modelo ARIMA(1,0,1)(0,1,0)[365] presenta el mejor ajuste a la série temporal con respecto a la variable temperatura media.

Figura 3: Gráfico de Residuales para el Modelo SARIMA. Fuente: Elaboración propia.

En la figura 3, además de la gráfica de autocorrelación ACF de los residuos estandarizados, es posible verificar la homogeneidad de los mismos. El gráfico muestra qué tan bien se ajusta el modelo a los datos. Se nota a través de la figura 3 que los residuos presentan una distribución aleatoria sin mostrar una tendencia. Por lo tanto, los residuos son ruido blanco, verificado a través de la prueba Ljung −Box = 0.346 y con AIC = 6088.59, en el análisis gráfico que los residuos se distribuyen de forma homogénea.

Figura 4: Gráfico de predicción con el modelo Sarima para nuestro banco de datos. Fuente: Elaboración propia.

En la figura 4, se puede observar la predicción que se ajustó con el modelo SARIMA a los datos meteorológicos de nuestro banco de datos. vemos que los valores ajustados están muy cerca de los reales, lo que significa que el modelo logró ajustarse bien a la serie, con un error cuadrático medio, MSE=0.87421.

Figura 5: Gráfico del mejor lambda ajustado con el método LASSO. Fuente: Elaboración propia.

En la figura 5, podemos observar la gráfica de nuestro mejor lambda (factor de penalización) para nuestro mejor modelo ajustado a nuestros datos, que en este caso nos dio -4.836514, el cual se encuentra dentro de las líneas punteadas, y se obtuvo mediante el método de LASSO. Este valor es muy importante, ya que nos permite obtener el mejor modelo para nuestros datos, el cual nos indica que el modelo ajustado es el óptimo. En caso de que tengamos valores muy altos o muy bajos con relación al valor de nuestro mejor lambda, nos indicaría que nuestro modelo no es el óptimo para nuestro datos.

CONCLUSIÓN

En nuestra data de meteorología se usaron los modelos ARIMA, SARIMA y el método de selección de variables LASSO para la predicción y su modelamiento, también se usó las pruebas de Dickey Fuller y Ljung Box para poder probar la estacionariedad y ruido blanco de nuestra serie temporal, haciendo uso del lenguaje de programación R para la estimación de los coeficientes. Se hizo una comparación de estos dos modelos para determinar cuál de ellas es la más adecuada para representar la serie original y estimar la valores futuros, observando que el modelo SARIMA tiene un mejor ajuste y mejor predicción de su comportamiento. 

BIBLIOGRAFÍA

[1] Ranstam, J., & Cook, J. A. (2018). LASSO regression. Journal of British Surgery, 105(10), 1348-1348. 

[2] Yan, Z., & Yao, Y. (2015). Variable selection method for fault isolation using least absolute shrinkage and selection operator (LASSO). Chemometrics and Intelligent Laboratory Systems, 146, 136-146. 

[3] Sun, K., Huang, S. H., Wong, D. S. H., & Jang, S. S. (2016). Design and application of a variable selection method for multilayer perceptron neural network with LASSO. IEEE transactions on neural networks and learning systems, 28(6), 1386-1396

[4] Kajuru, J. Y., Abdulkarim, K.,& Muhammed, M. M. (2019). Forecasting Performance of ARIMA and Sarima Models on Monthly Average Temperature of Zaria, Nigeria. ATBU Journal of Science, Technology and Education, 7(3), 205-212. 

[5] Otu, O. A., Osuji, G. A., Opara, J., Mbachu, H. I., & Iheagwara, A. I. (2014). Application of Sarima models in modelling and forecasting Nigeria’s inflation rates. American Journal of Applied Mathematics and Statistics, 2(1), 16-28.

[6] Tseng, F. M., Yu, H. C., & Tzeng, G. H. (2002). Combining neural network model with seasonal time series ARIMA model. Technological forecasting and social change, 69(1), 71-87.

[7] Rodrigues, K. A. (2018). LASSO Clássico e Bayesiano. Instituto de Matemática e Estatística,Universidade de São Paulo, Brasil.

[8] Instituto Nacional de Meteorologia, Ministério da Agricultura, Pecuária e Abastecimento, Brasil.  (https://portal.inmet.gov.br/dadoshistoricos).