Algoritmos de optimización convexa para Aprendizaje automático

Existe una gran variedad de algoritmos de aprendizaje automáticos en las distintas áreas de investigación que son desarrollados con la teoría de optimización convexa en donde vemos las matemáticas

Algoritmos de optimización convexa para Aprendizaje automático

Por Daniel Mavilo Calderon Nieto

Los intentos de aplicar métodos matemáticos a la extracción de información de los datos se remontan al trabajo de Boscovich [21], Gauss [22], Laplace [23] y Legendre [24]. Así, en relación con el problema de estimar parámetros a partir de observaciones ruidosas, Boscovich y Laplace inventaron el método de ajuste de datos de desviaciones mínimas, mientras que Legendre y Gauss inventaron el método de ajuste de datos de mínimos cuadrados. En el lado algorítmico, el método de gradiente fue inventado por Cauchy [25] para resolver un problema de ajuste de datos en astronomía y desde entonces se han utilizado métodos más o menos heurísticos.

La optimización convexa trata el problema general de minimizar una función convexa, sobre un conjunto también convexo [30]. Hoy en día, optimización convexa general los métodos han penetrado prácticamente en todas las ramas de la ciencia de datos [26], [27], [28], [29]. Muchos de los avances recientes en algoritmos de optimización convexa han sido motivados por problemas de procesamiento de datos en la recuperación de señales, problemas inversos, o aprendizaje automático. Al mismo tiempo, el diseño y el análisis de convergencia de algunos de los métodos de división (métodos que descomponen o permiten la solución de problemas no lineales ) más potentes en optimización altamente estructurada o a gran escala están basados en conceptos que no se encuentran en la caja de herramientas de optimización tradicional pero que profundizan en el análisis no lineal [7].

Algunos algoritmos de optimización convexa para aprendizaje automático y su aplicación en las áreas de investigación son: en Ingeniería, “Algoritmos genéticos interactivos (IGAs) [1] y algoritmo de controlador de estimación de movimiento [12],” en Ciencias de la computación, “Algoritmo estocástico de optimización de punto fijo [3], algoritmo de gradiente proximal dual descentralizado síncrono (SynDe-DuPro) [6] y el algoritmo de SVM de mínimos cuadrados (LSSVM) [8],” en Matemática, “Algoritmo de optimización convexa de bandidos [16], algoritmo del plano de corte [18],” en Geociencias,  “ en Geociencias, “Algoritmo de optimización de ballenas mejorado [19],” y en Economía, finanzas y negocios, “Algoritmo de optimización de enjambre de partículas [2].”

Aplicaciones

Podemos notar que las condiciones y definición de la optimización convexa son usadas en distintos modelos o algoritmos para el aprendizaje automático [5, 7]. Uno de los métodos o algoritmos más utilizados en el aprendizaje automático para clasificación y que usan optimización convexa son las máquinas de vectores de soporte (SVM,  por sus siglas en inglés)  [9, 10, 14]. En la figura 1 veremos la metodología empleada en los algoritmos genéticos interactivos (IGA, por sus siglas en inglés).

Figura 1. Diagrama de flujo de la metodología IGA [1].

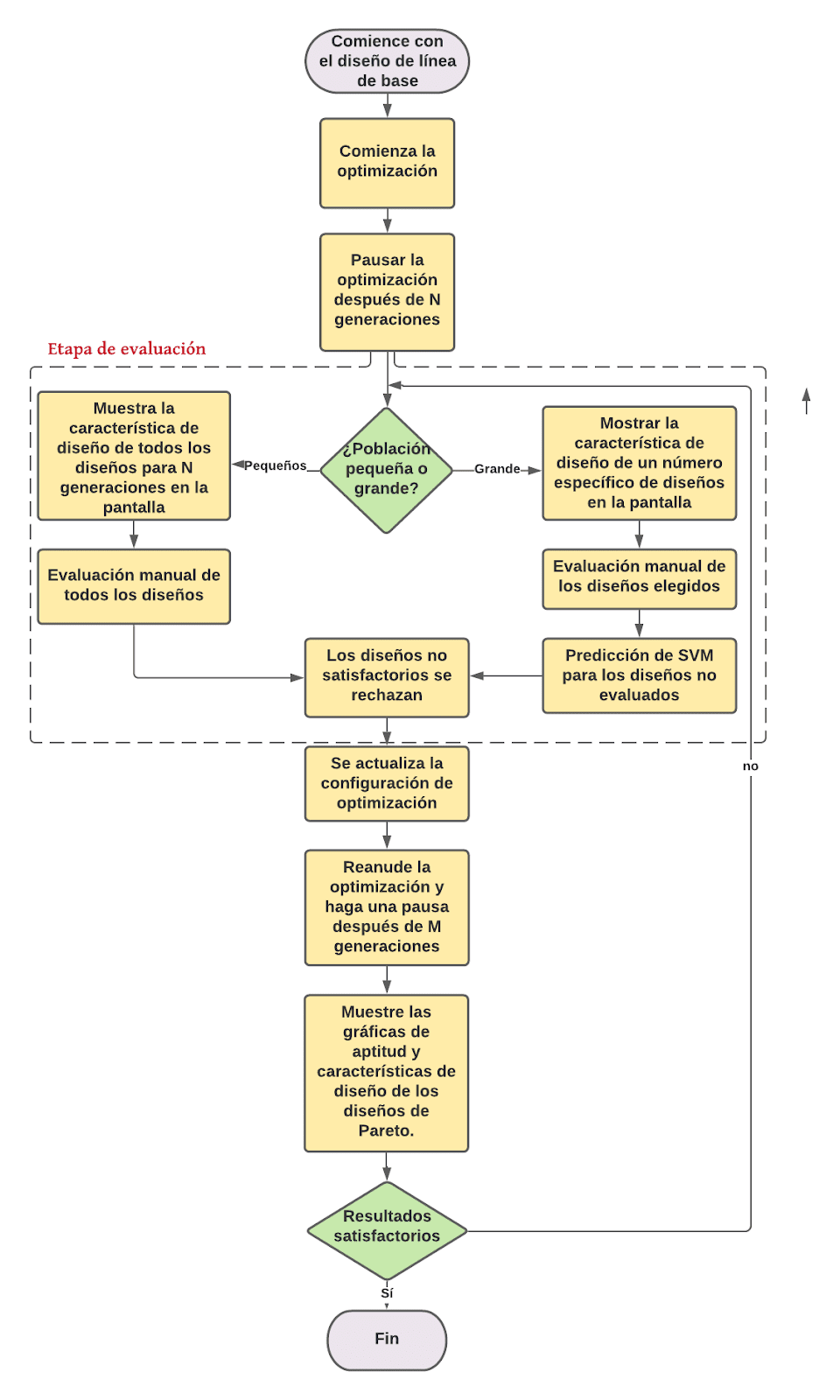
En la Figura 2 se presenta un diagrama de flujo de la metodología IGA implementada por el objetivo de producir varias alternativas de diseño, presentar algunas de sus características de diseño a los usuarios para su evaluación manual y agregar esa información de usuario al método de optimización para guiarlo a áreas del espacio de diseño que ofrecerán diseños más adecuados. Antes de iniciar la optimización, se crea manualmente un diseño de hoja, lo que se denomina diseño de línea base, y el objetivo es aumentar el rendimiento de la misma de la mejor manera posible. Para aumentar el rendimiento, se crean varios diseños con pequeñas alteraciones geométricas a través del algoritmo de optimización. Los usuarios ejecutan el algoritmo de optimización y, en cierto punto, se les pide que evalúen interactivamente algunas limitaciones cualitativas del problema. Cuando los usuarios hayan terminado con las evaluaciones manuales, pueden optar por continuar el proceso de optimización seleccionando diseños que les parezcan interesantes para una mayor evolución. Este procedimiento se repite hasta que se obtienen los resultados deseables.

Más detalladamente, el proceso de optimización comienza con una ronda de optimización utilizando el algoritmo genético de clasificación no dominado elitista (NSGA-II, por sus siglas en inglés). Cada proceso de optimización generalmente consta de varios ciclos de optimización más pequeños, las rondas de optimización, que duran desde iniciarlos con una nueva configuración o entrada hasta pausarlos manualmente o finalizar el ciclo. Los usuarios pre definen el número de generaciones, individuos por generación, objetivos, limitaciones, variables de diseño y parámetros de optimización. Las variables de diseño de la optimización oscilan entre un límite superior e inferior en relación con los valores de las variables de diseño del diseño de línea de base.

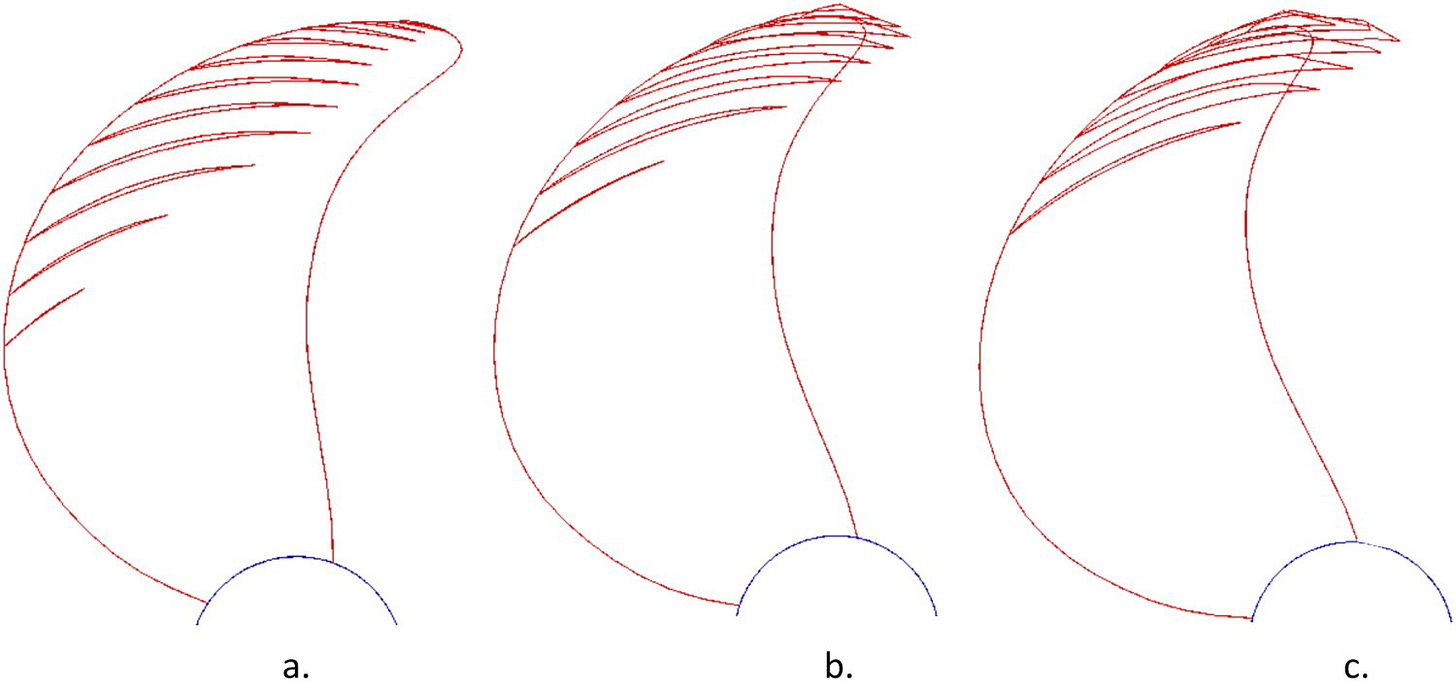
Después de un número preestablecido de generaciones (N), la optimización se detiene y sigue la etapa de evaluación, donde hay dos opciones. Si la población de los diseños individuales es grande, entonces se presenta a los usuarios una parte más pequeña de la población total. Esta parte consta de diseños únicos que se seleccionan al azar de las generaciones totales hasta ese momento. Si la población es pequeña, se presentan todos los diseños. La información que se muestra en la pantalla, en el escenario específico, es la forma de la cavidad que se ha desarrollado en la pala de cada hélice individual, como se muestra en la Figura 2. Tanto para poblaciones pequeñas como grandes de individuos, los usuarios evalúan los diseños en la pantalla rechazándolos o aceptándolos, de acuerdo con sus propias preferencias y experiencia de diseño. En el caso de una población grande, los usuarios evalúan una parte más pequeña de la población total, mientras que se hace una predicción para el resto de los individuos mediante un modelo SVM. Como se mencionó anteriormente, el modelo SVM se utiliza para evitar la fatiga del usuario por tener que evaluar demasiados diseños. Para ambos casos, se rechazan los diseños no satisfactorios.

Figura 2: Forma de la cavidad de tres hélices en el ángulo del volumen máximo de la cavidad [1].

Al final de la etapa de evaluación, los usuarios tienen la posibilidad de actualizar la configuración para la optimización continua, por ejemplo, número de generaciones, individuos por generación, objetivos, restricciones, variables de diseño y parámetros de optimización. Si el número requerido de individuos para la siguiente ronda es mayor que el número de diseños aceptados, entonces la mutación y el cruce se utilizan para que los individuos aceptados creen otros nuevos con el fin de completar los individuos que faltan; si el número es menor, los individuos aceptados se clasifican y las soluciones no dominadas se mantienen, de manera similar a la NSGA-II; si el número es igual, entonces la primera generación está compuesta por todos los diseños aceptados previamente.

Cuando se ha creado la primera generación de la segunda ronda de optimización, se reanuda la optimización. La optimización se vuelve a pausar después de un número M de generaciones y los diseños de la frontera de Pareto, junto con las correspondientes parcelas de cavitación, se muestran en la pantalla. Si los resultados son satisfactorios, todo el proceso está terminado; de lo contrario, el ciclo vuelve a la etapa de evaluación. Este proceso se repite hasta que se logran los resultados deseables.

 Los algoritmos de optimización siguen siendo desarrollados y mejorados en la actualidad con diferentes objetivos, por ejemplo, la minimización del costo en una red de computación [13], la recuperación de fase en diversos campos de aplicación de la ciencia e ingeniería [15] y también se entrena a un conjunto de datos de enfermedades hepáticas [17].

Conclusión

El aprendizaje automático en el transcurso de estos años ha venido generando nuevas y novedosas formas de solucionar problemas o predecir resultados en diferentes áreas de investigación. Actualmente sigue en crecimiento el desarrollo de nuevos algoritmos y modelos matemáticos que permitan mejorar los ya existentes o crear nuevos y con ellos lograr que el aprendizaje automático sea una alternativa de solución en nuevas áreas de investigación. Notar que las matemáticas han aportado y siguen haciéndolo a través de algoritmos de optimización.

Referencias

[1] Ioli, G., Marcus, J., Krister W., and Rickard B., “Propeller optimization by interactive genetic algorithms and machine learning," Ship Technology Research, 2021.

[2] Tian, Z., Ren, Y., and Wang, G., ”Short-term wind speed prediction based on improved PSO algorithm optimized EM-ELM.,” Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, pp. 1–21, 2018. 

[3] Iiduka, H., ”Stochastic Fixed Point Optimization Algorithm for Classifier Ensemble,” IEEE Transactions on Cybernetics, pp. 1–11, 2019.

[4] Li, H., Fang, C., and Lin, Z., “Accelerated First-Order Optimization Algorithms for Machine Learning,” Proceedings of the IEEE, pp. 1–16, 2020.

[5] Lesage-Landry, A., Shames, I., & Taylor, J. A., “Predictive online convex optimization. Automática,” vol. 113, pp. 10877, 2020.

[6] Li, H., Hu, J., Ran, L., Wang, Z., Lu, Q., Du, Z., and Huang, T., “Decentralized Dual Proximal Gradient Algorithms for Non-Smooth Constrained Composite Optimization Problems,” IEEE Transactions on Parallel and Distributed Systems, vol. 32(10), pp. 2594–2605, 2021

[7] Combettes, P. L., and Pesquet, J.-C., “Fixed Point Strategies in Data Science,” IEEE Transactions on Signal Processing, vol. 69, pp. 3878–3905, 2021.

[8] Chorowski, J., Wang, J., and Zurada, J. M., ”Review and performance comparison of SVM- and ELM-based classifiers,” Neurocomputing, vol. 128, pp. 507–516, 2014.

[9] Khemchandani, R., Jayadeva, and Chandra, S., “Learning the optimal kernel for Fisher discriminant analysis via second order cone programming,” European Journal of Operational Research, vol. 203(3), pp. 692–697, 2020.

[10] Kim, S.-J., Zymnis, A., Magnani, A., Kwangmoo Koh, and Boyd, S. “ Learning the kernel via convex optimization,” IEEE International Conference on Acoustics, Speech and Signal Processing. 2008.

[11] Cutkosky, A., Busa-Fekete, R., “Distributed stochastic optimization via adaptive SGD,” Advances in Neural Information Processing Systems, pp. 1910-1919, Dec. 2018.

[12] Hsieh, J.-H., and Wang, H.-R., “VLSI Design of an ML-Based Power-Efficient Motion Estimation Controller for Intelligent Mobile Systems,” IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 26(2), pp. 262–271, 2018.

[13] Wang, D., and Zhao, J., “Computation Offloading and Resource Allocation in Mobile Edge Computing via Reinforcement Learning,” 11th International Conference on Wireless Communications and Signal Processing (WCSP), 2019.

[14] Yang, J., Liu, L., Zhang, L., Li, G., Sun, Z., and Song, H., “Prediction of Marine Pycnocline Based on Kernel Support Vector Machine and Convex Optimization Technology,” Sensors, vol. 19(7), pp. 1562, 2019.

[15] Liu, J.-W., Cao, Z.-J., Liu, J., Luo, X.-L., Li, W.-M., Ito, N., and Guo, L.-C., ”Phase Retrieval via Wirtinger Flow Algorithm and Its Variants,” International Conference on Machine Learning and Cybernetics (ICMLC), 2019.

[16] Boumerdassi, S., Renault, É., and Mühlethaler, P. (Eds.)., “Machine Learning for Networking,” Lecture Notes in Computer Science, 2020.

[17] Joshi, N., and Tammana, R., “GDALR: An Efficient Model Duplication Attack on Black Box Machine Learning Models,” IEEE International Conference on System, Computation, Automation and Networking (ICSCAN), 2019.

[18] Xiao, F., and Zhou, J., “Optimized cutting plane method for training a structural SVM,” Qinghua Daxue Xuebao/Journal of Tsinghua University, vol. 53 (7), pp. 1057-1063, 2013.

[19] Wang, C., Zhu, Z., Chen, S., and Yang, J., “Illumination correction via support vector regression based on improved whale optimization algorithm,” Color Research & Application, 2020.

[20] R. J. Boscovich, “De literaria expeditione per pontificiam ditionem et synopsis amplioris operis..., Bononiensi Scientiarum et Artum Instituto atque Academia Commentarii, vol. 4, pp. 353–396, 1757.

[21] C. F. Gauss, “Theoria Motus Corporum Coelestium,” Hamburg: Perthes and Besser, 1809.

[22] P. S. Laplace, Sur quelques points du système du monde, Mémoires Acad. Royale Sci. Paris, pp. 1–87, 1789.

[23] A. M. Legendre, “Nouvelles Méthodes pour la Détermination des Orbites des Cométes,” Firmin Didot, Paris, 1805.

[24] A. Cauchy, “Méthode générale pour la résolution des systèmes d'équations simultanées,” C. R. Acad. Sci. Paris, vol. 25, pp. 536– 538, 1847.

[25] E. Artzy, T. Elfving, and G. T. Herman, “Quadratic optimization for image reconstruction II,” Comput. Graph. Image Process., vol. 11, pp. 242–261, 1979.

[26] C. L. Byrne, “Iterative Optimization in Inverse Problems,” Boca Raton, FL: CRC Press, 2014.

[27] A. Chambolle and T. Pock, “An introduction to continuous optimization for imaging,” Acta Numer., vol. 25, pp. 161–319, 2016.

[28] P. L. Combettes, “The convex feasibility problem in image recovery, in: Advances in Imaging and Electron Physics,” (P. Hawkes, Ed.), vol. 95, pp. 155–270. New York: Academic Press, 1996.

[29] S. Sra, S. Nowozin, and S. J. Wright, “Optimization for Machine Learning,” MIT Press, Cambridge, MA, 2012.

[30] Candès, E.J., Recht, B., “Exact matrix completion via convex optimization,” Foundations of Computational Mathematics, vol. 9 (6), pp. 717-772, 2009.